Aufgabe Einheitsvektoren

 

Berechnen Sie das Kreuzprodukt zweier Vektoren

 

 

Lösung:

>>e_1 = [1;0;0];

>>e_2 = [0;1;0];

>>e_3 = cross(e_1,e_2)


e_3 =

0
0
1


 

Aufgabe Skalarprodukt

 

Multiplizieren Sie zunächst den Vektor x₁ mit drei. Addieren Sie anschließend den Vektor a und ersetzen Sie die mittlere Zahl durch 14. Zum Schluss bilden Sie das Skalarprodukt aus dem eben entstandenen Vektor und dem Vektor x₂.

 

 

Speichern Sie das Ergebnis in die Variable x₃. Überlegen sie, welche Variable Sie für die Zwischenspeicherung des ersten Vektors nutzen.

 

Lösung:

>> x_1 = [9;5;3];

>> a = [4;1;0];

>> x_2 = [1;0;4];

>> x_1.*3;

>> ans+a;

>> ans(2) = 14;

>> x_3 = dot(ans,x_2)


x_3 =

67

 

Aufgabe Transponieren

 

Gegeben sei der Zeilenvektoren x und der Spaltenvektor y. Ersetzen sie das zweite und das dritte Element des Vektors x mit 3 und 7. Transponieren sie danach den Vektor x und multiplizieren Sie ihn elementweise mit y.

 

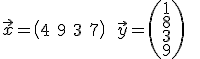
>>x = [4, 9, 3, 7];

>>y = [1;8;3;9];

>>x(2) = 3;

>>x(3) = 7;

>>x = x';

>>x.*y


ans =

4
24
21
63